Nous connaissons tous :
Pi : 3,14 mais connaissez-vous φ (Phi ) : 1,6180339887 ?
Qu'est-ce que Phi ?
- Son nom : hommage rendu au sculpteur grec Phidias qui décora le Parthénon.
- Sa formule : (1+√5)/2≃1,6180339887
Phi est considérée comme une formule universelle de la beauté. Ce nombre permet de réaliser des compositions équilibrées, régit des rapports harmonieux. Phi est en réalité le résultat de la division de deux longueurs, c’est donc une proportion. La proportion est dite d’or (ou divine) lorsque le rapport entre la petite et la grande partie est identique au rapport entre le grand rapport et le tout.
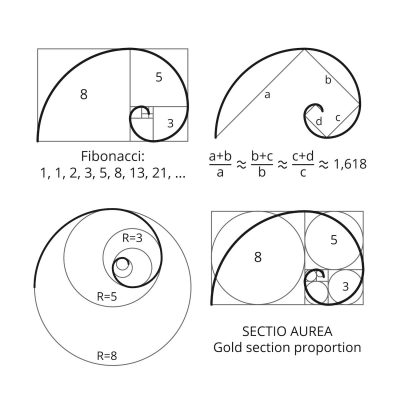
Phi est associée à la suite de Fibonacci. (Mathématicien Pisan du XII) La suite de Fibonacci (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,…) est une suite de nombre tel qu’un nombre est égal à la somme des deux précédents, en prenant les deux premiers nombres égaux à 1.
Phi s’associe avec des outils géométriques :
– rectangle d’or, spirale d’or et angle d’or
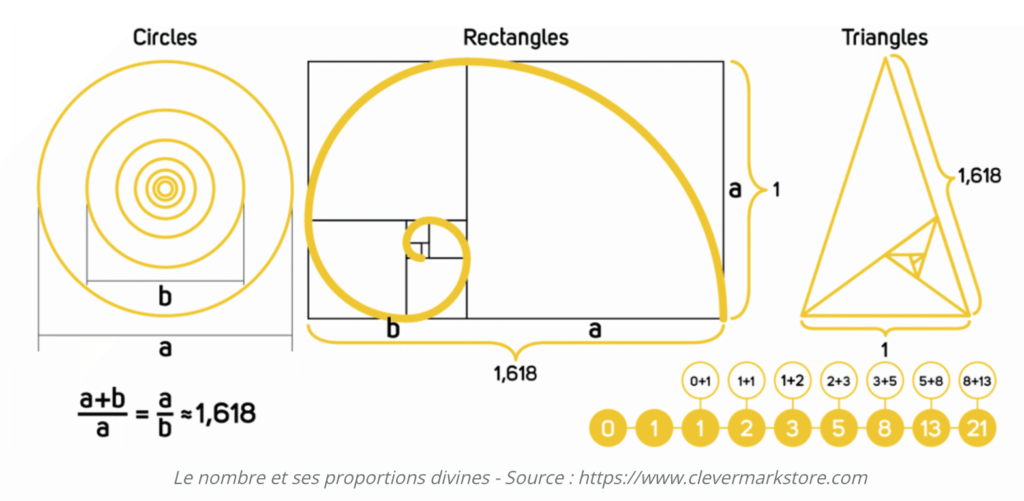
Phi et la théorie
Ce nombre est mentionné pour la première fois dans les Éléments, un traité de mathématiques et de géométrie écrit par Euclide vers l’an 300 avant J.-C.
Mais c’est à la suite de la publication en 1509 du traité « de divina proportione » du mathématicien Luca Pacioli et illustré par des planches de Léonard de Vinci, que les artistes et mathématiciens s’approprient pleinement ce nombre irrationnel.
Phi organisateur des oeuvres d’art
De nombreux artistes (peintre, architecte, designer) s’appuient sur Phi pour réaliser leurs œuvres. Cette proportion est simplement agréable à regarder pour l’œil humain.
Voici des exemples dans des oeuvres architecturales, picturales et design :
– Les bâtisseurs de la pyramide de Kheops connaissaient le nombre d’or. En effet, le rapport de la hauteur de la pyramide, mesurée par Thalès, par sa demi base est égal au nombre d’or.
– Le Parthénon datant de 490 à 430 av. J-C. est construit avec ce nombre.
– Le théâtre d’Épidaure, IVème siècle av. J.-C. possède deux séries de gradins, 21 et 34, deux nombres consécutifs de la suite de Fibonacci.
– Le Corbusier use du nombre d’or dans le Modulor, système de proportions du corps humain, pour équilibrer ses constructions.
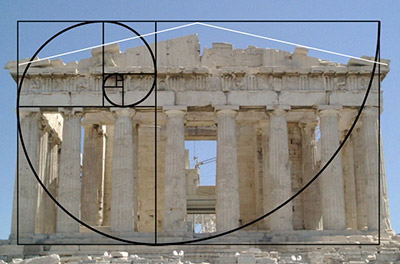
Parthénon (Grèce)
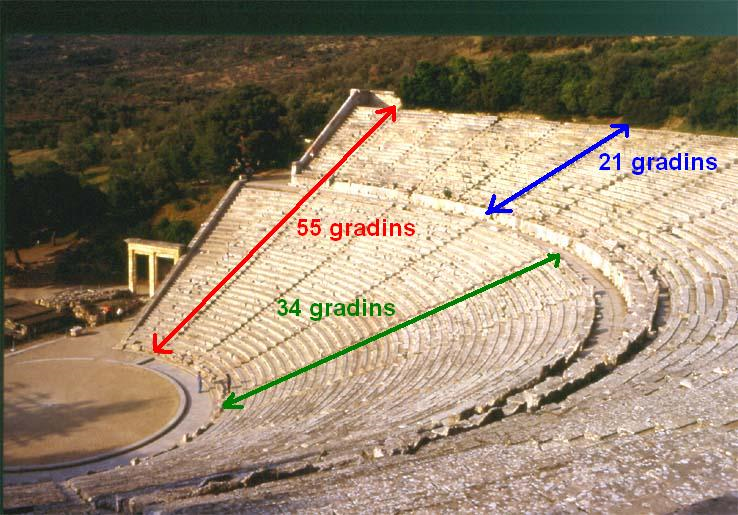
Gradins du théâtre d’Epidaure (Grèce)
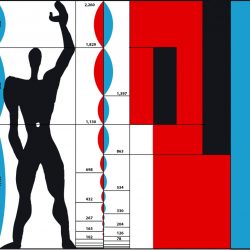
Image @ Fondation Le Corbusier (Modulor ou le nombre d’or dans l’habitat)

La naissance de Vénus de Sandro Botticelli
Les dimensions sont de 172.5×278.5cm. Le rapport entre la longueur et la largeur est 278,5 /172,5=1,61….. soit environ le nombre d’or φ

La vague de Kanagawa – Estampe de Katsushika Hokusai
Spirale d’or pour composer la vague

La flagellation du Christ de Piero della Francesca
Parfait triangle d’or qui régit la construction du tableau
Design/graphisme et logos
Nombreux logos suivent ce fil conducteur mathématique pour devenir plus efficaces, équilibrés et percutants. (Pepsi, Toyota, Apple, etc.)
En effet, les designers/graphistes élaborent la construction de logos avec une grille… dite “grille d’or”.
Très proche de la règle des tiers, elle divise différemment l’image pour créer une composition plus puissante et plus naturelle. (Avec la règle des tiers, l’image est en effet divisée en deux lignes horizontales coupant deux lignes verticales – Les photographes utilisent cette règle de tiers pour composer leurs clichés).
Les points d’intérêts de la scène se placent aux intersections de l’une des lignes.

Grille d’or (proche de la règle des tiers)
En plus de la grille, la spirale de Fibonacci se décompose et favorise des outils de proportions. La règle 1/3-2/3 que graphistes ou designers utilisent fréquemment.
Logos construits avec Phi

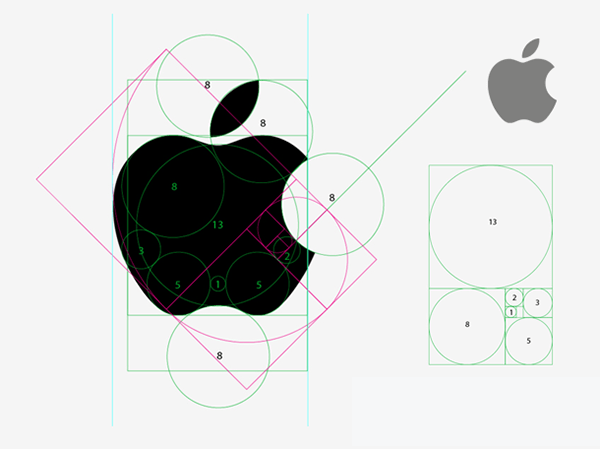

La longueur et la largeur du rectangle ont un ratio de 1,61.
Les courbes du logo sont des cercles aux diamètres proportionnés réalisées grâce à la suite de Fibonacci.
Logo réalisé avec la spirale d’or – Source Dribbble
Phi et la nature en guise de conclusion
Le nombre d’or se définit comme la clé de l’harmonie universelle.
Proportion qui se retrouve également dans la nature.
La phyllotaxie (l’art de la disposition des feuilles sur une tige) atteste cette présence de spirales. Regardez un tournesol ou des pommes de pin.